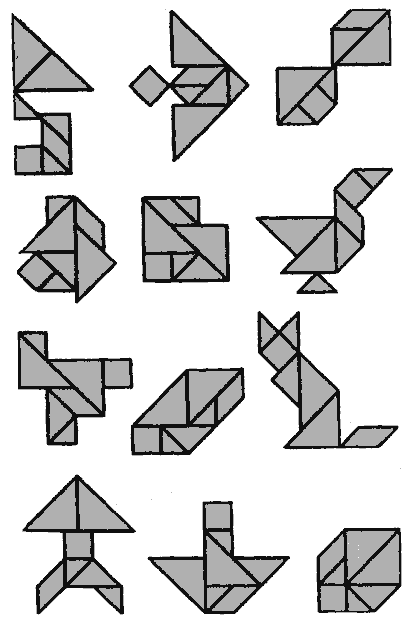
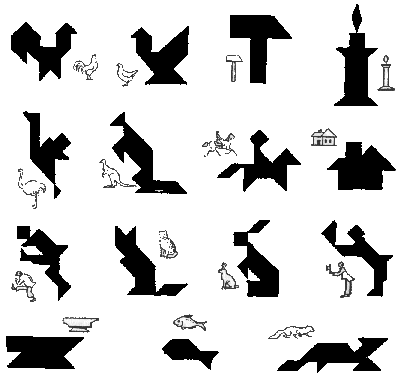
Танграм («семь дощечек мастерства») — - старинная китайская игра-головоломка. Головоломка состоит из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться между собой.
 История Танграм
История ТанграмТанграм, возможно, ведёт своё происхождение от яньцзиту (燕几圖) — вида мебели, появившегося во времена империи Сун. Как мебель яньцзиту претерпела некоторые изменения за время правления династии Мин, а в дальнейшем превратилась в набор деревянных фигурок для игры.
Хотя танграм часто считают изобретением глубокой древности, первое печатное упоминание о нём встречается в китайской книге, изданной в 1813 году и написанной, очевидно, в правление императора Цзяцина.
Появление танграма на западе относят не ранее чем к началу 19 столетия, когда эти головоломки попали в Америку на китайских и американских судах. Старейший такой экземпляр, подаренный сыну американского судовладельца в 1802 году, сделан из слоновой кости и хранится в шёлковом футляре.
Слово «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии».
Писатель и математик Льюис Кэролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.
У Наполеона во время его изгнания на остров Святой Елены был набор для танграма и книга, содержащая задачи и решения. Фотографии этого набора содержатся в книге Джерри Слокума The Tangram Book.
Книга Сэма Лойда The Eighth Book Of Tan (англ. «Восьмая книга Тан»), вышедшая в 1903 году, содержит вымышленную историю танграма, согласно которой эта головоломка была изобретена 4000 лет назад божеством по имени Тан. Книга включает 700 задач, некоторые из которых неразрешимы.
Парадоксы ТанграмПарадокс танграма заключается в следующем: каждый раз полностью используя весь набор, можно сложить две фигуры, одна из которых будет подмножеством другой. Один такой случай приписывается Дьюдни: две похожие фигуры изображают монахов, но у одной из них при этом есть нога, а у другой фигуры её нет. Разрешение этого парадокса приводится во многих источниках.
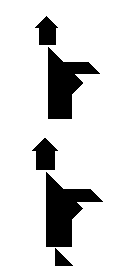
Другой парадокс предлагается Лойдом в «Восьмой книге Тан»:
Цитата:
Седьмая и восьмая фигуры изображают загадочный квадрат, составленный из семи частей. Затем угол квадрата срезали, но при этом всё равно используются те же семь частей.
Решение данного парадокса не приводится в книге Лойда.
 Подсчёт конфигураций
Подсчёт конфигурацийВан Футрайн и Сюн Цюаньчжи (熊全治) доказали в 1942 году, что существуют только пятнадцать выпуклых конфигураций танграма (таких, что отрезок прямой, проведённый между любыми двумя точками внешнего контура, пройдёт только через точки, заключённые внутри этого контура; иными словами — без пустот посередине).
Книга Рональда Рида Tangrams: 330 Puzzles (англ. Танграм: 330 задач) просит читателей присылать любые другие фигуры. Такое условие создаёт множество хотя и с гораздо большим числом элементов, чем множество выпуклых фигур, но всё же конечное.
В ответ было предложено приблизительно 6,13 миллиона возможных конфигураций, в каждой из которых при этом хотя бы одна вершина и хотя бы одна сторона любой части совпадают с вершиной и стороной другой части.
ФигурыРазмеры приведены относительно большого квадрата, стороны и площадь которого принимают равными.
-5 прямоугольных треугольников
2 маленьких (с гипотенузой, равной 1/2 и сторонами √2/4 )
1 средний (гипотенуза 1/√2 и стороны 1/2)
2 больших (гипотенуза 1 и стороны 1/√2 )
-1 квадрат (со стороной √2/4 )
-1 параллелограмм (со сторонами 1/2 и √2/4)
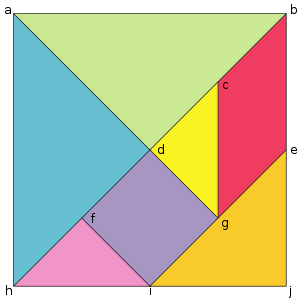
Среди этих семи частей параллелограмм выделяется отсутствием у него зеркальной симметрии (он обладает только вращательной симметрией), так что его зеркальное отражение можно получить, только перевернув его. Это единственная часть танграма, которую требуется перевернуть, чтобы сложить определённые фигуры. При использовании одностороннего набора (в котором переворачивать фигуры запрещено) есть фигуры, которые можно сложить, в то время как их зеркальное отражение — нельзя.
Педагогическое значение танграмаСпособствует развитию у детей умения играть по правилам и выполнять инструкции, наглядно-образного мышления, воображения, внимания, понимания цвета, величины и формы, восприятия, комбинаторных способностей.
Примеры и правила сложений танграмаПравила этой игры просты. В состав каждой фигурки должны входить все семь частей; при этом они не должны перекрываться. Ниже представлены некоторые фигурки, которые можно сложить из 7 кусочков танграма.